Grundlagen der Chromatografie - Verteilung
Schüttelt man eine wässrige Iodlösung mit dem gleichen Volumen an Tetrachlormethan, so wird der größte Teil des Iods von der organischen Phase aufgenommen. Es stellt sich bei konstanter Temperatur ein Gleichgewicht der Verteilung des Iods zwischen den beiden nicht mischbaren flüssigen Phasen ein.
Das Verhältnis der Stoffmengenkonzentration in den beiden Phasen ergibt den Verteilungskoeffizienten K.
Bei der Verteilung eines Stoffes zwischen zwei Phasen nimmt das Verhältnis seiner Stoffmengenkonzentration bei konstanter Temperatur einen konstanten Wert an. Dieses Verteilungsgesetz gilt nur für den Fall, dass der gelöste Stoff in beiden Phasen in der gleichen Form (Aggregatzustand) vorliegt. Er darf nicht dissoziieren, dimerisieren oder Addukte mit dem Lösungsmittel bilden.
In der Praxis ist das Ausschütteln oder die diskontinuierliche Extraktion organischer Verbindungen der wichtigste Mechanismus. Die Lösung eines Stoffgemisches wird in einen Scheidetrichter gegeben und mit einer nicht mischbaren Flüssigkeit versetzt. In dem zugesetzten Lösungsmittel sollte sich der abzutrennende Stoff gut lösen.
Das Verhältnis der Stoffmengenkonzentration in den beiden Phasen ergibt den Verteilungskoeffizienten K.
| Verteilungsgesetz nach Nernst: K = | Konzentration in Phase 1
Konzentration in Phase 2 |
Bei der Verteilung eines Stoffes zwischen zwei Phasen nimmt das Verhältnis seiner Stoffmengenkonzentration bei konstanter Temperatur einen konstanten Wert an. Dieses Verteilungsgesetz gilt nur für den Fall, dass der gelöste Stoff in beiden Phasen in der gleichen Form (Aggregatzustand) vorliegt. Er darf nicht dissoziieren, dimerisieren oder Addukte mit dem Lösungsmittel bilden.
In der Praxis ist das Ausschütteln oder die diskontinuierliche Extraktion organischer Verbindungen der wichtigste Mechanismus. Die Lösung eines Stoffgemisches wird in einen Scheidetrichter gegeben und mit einer nicht mischbaren Flüssigkeit versetzt. In dem zugesetzten Lösungsmittel sollte sich der abzutrennende Stoff gut lösen.
Rechnerische Simulation zur Verteilung
Die Trennung zweier Komponenten durch Verteilung in verschiedenen Zeitabschnitten soll hier verdeutlicht werden. Die oberen Kästchen sollen jeweils die mobile Phase (MP), die unteren die stationäre (SP) darstellen. Die Stoffe sollen sich nach einem festen Zahlenverhältnis auf die Phasen verteilen:
Die roten Teilchen verteilen sich im Verhältnis 1 /2 auf die mobile und stationäre Phase, die blauen Teilchen 2/1.
Benutzen Sie bitte für die Bearbeitung zwei Stifte mit unterschiedlichen Farben! Schreiben Sie die Teilchenzahl von Stoff 1 mit der ersten Farbe immer links in das Kästchen, die Teilchenzahl von Stoff 2 mit der zweiten Farbe immer rechts in das Kästchen!
1. Zunächst sind jeweils 81 Teilchen von jeder Sorte in die oberen Phase (Ort 1, oberstes Kästchen) "eingefüllt" (links 81 und rechts 81 hingeschrieben).
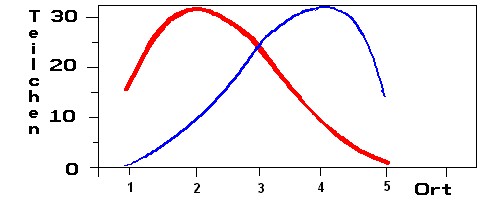
In Schritt 2 verteilt sich Stoff 1 am Ort 1 auf beide Phasen bis sich das Gleichgewicht 1:2 eingestellt hat (links oben: 27, unten: 54). Der zweite Stoff verteilt sich entsprechend (rechts oben 54, unten 27). Die mobile Phase schiebt die oberen Teilchen von Ort 1 nach Ort 2 (links oben27 und rechts oben 54) - unten bleibt noch frei. An Ort 1 verbleiben unten links 54 und rechts 27 (oben: frei). Dann werden die Teilchen am Ort (oben und unten) aufsummiert und neu verteilt und so weiter.... Zeichnen Sie zum Schluss die Summe der Teilchen am jeweiligen Ort (übereinander stehende Kästchen) mit den jeweiligen Farben in das Koordinatensystem ein!
| Komponente 1 | Komponente 2 | |
| mobile Phase | 1 | 2 |
| Stationäre Phase | 2 | 1 |
Die roten Teilchen verteilen sich im Verhältnis 1 /2 auf die mobile und stationäre Phase, die blauen Teilchen 2/1.
Benutzen Sie bitte für die Bearbeitung zwei Stifte mit unterschiedlichen Farben! Schreiben Sie die Teilchenzahl von Stoff 1 mit der ersten Farbe immer links in das Kästchen, die Teilchenzahl von Stoff 2 mit der zweiten Farbe immer rechts in das Kästchen!
1. Zunächst sind jeweils 81 Teilchen von jeder Sorte in die oberen Phase (Ort 1, oberstes Kästchen) "eingefüllt" (links 81 und rechts 81 hingeschrieben).
In Schritt 2 verteilt sich Stoff 1 am Ort 1 auf beide Phasen bis sich das Gleichgewicht 1:2 eingestellt hat (links oben: 27, unten: 54). Der zweite Stoff verteilt sich entsprechend (rechts oben 54, unten 27). Die mobile Phase schiebt die oberen Teilchen von Ort 1 nach Ort 2 (links oben27 und rechts oben 54) - unten bleibt noch frei. An Ort 1 verbleiben unten links 54 und rechts 27 (oben: frei). Dann werden die Teilchen am Ort (oben und unten) aufsummiert und neu verteilt und so weiter.... Zeichnen Sie zum Schluss die Summe der Teilchen am jeweiligen Ort (übereinander stehende Kästchen) mit den jeweiligen Farben in das Koordinatensystem ein!